Making System Stacking Fingerprints (SSFs)

Making System Stacking Fingerprints (SSFs)#

This pipeline creates System Stacking Fingerprints (SSFs) like the one below which can be used to analyze system-wide pi-stacking in a molecular dynamics trajectory.

_images/SSF_test.png

Load Trajectory#

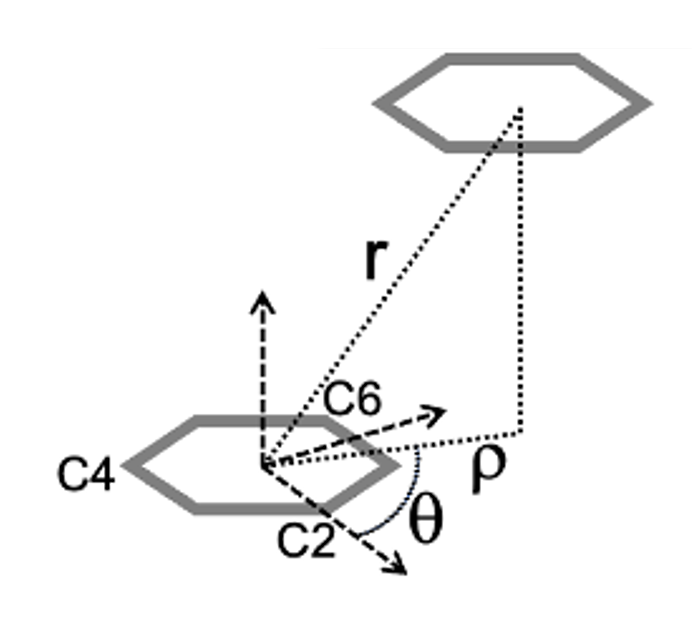
To analyze pi-stacking between two nucleotides, we compare their center of geometry (COG) distance, the distance between the centers of their 6-membered (pyrimidine) rings (see r below). For this, the only atoms we need are C2, C4, and C6 to triangulate the COG of each ring.

_images/bottaro_values.png

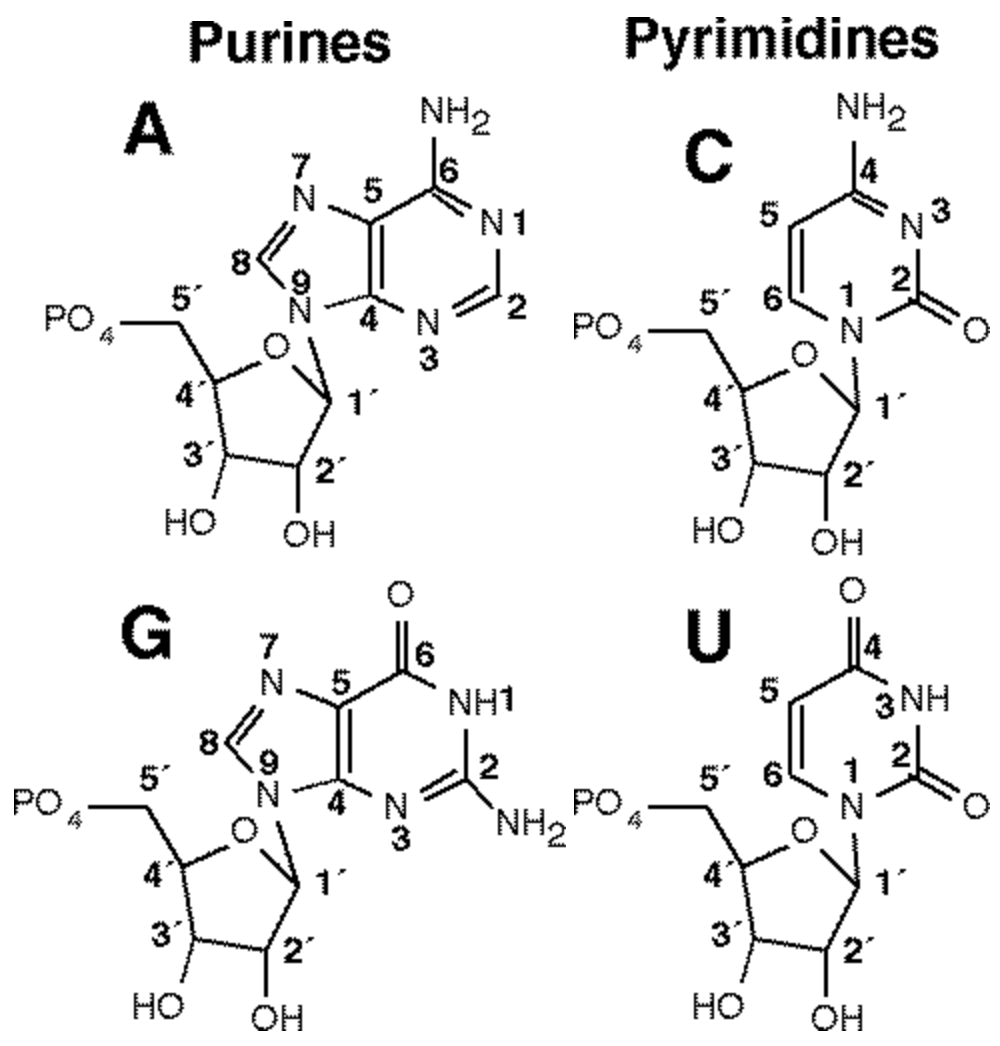
For reference, the Carbon Numbering of each nucleotide:

_images/nucleotide_numbering.png

In this example pipeline, we use a trajectory of the Ribosome CAR-mRNA Interaction Surface found in the StACKER GitHub Repository. We filter this trajectory to the pi-stacking residue pair.

MD Files are provided for testing convenience in the testing folder:

  • first10_5JUP_N2_tUAG_aCUA_+1GCU_nowat.mdcrd: A 10-frame trajectory file with all atoms/residues.

  • 5JUP_N2_tUAG_aCUA_+1GCU_nowat.prmtop: The associated Topology File with the above trajectory.

We filter to atoms C2, C4, and C6 using filter_traj():

>>> import stacker as st
>>> filtered_traj = st.filter_traj("first10_5JUP_N2_tUAG_aCUA_+1GCU_nowat.mdcrd",
...                 top_file = "5JUP_N2_tUAG_aCUA_+1GCU_nowat.prmtop",
...                 atoms = {"C2", "C4", "C6"})
WARNING: Residue Indices are expected to be 1-indexed
Reading trajectory...
Reading topology...
Filtering trajectory...
WARNING: Output filtered traj atom, residue, and chain indices are zero-indexed
>>> filtered_traj
<mdtraj.Trajectory with 10 frames, 756 atoms, 252 residues, without unitcells at 0x1164eab10>

Now the Python variable filtered_traj contains 10 frames of C2, C4, C6 information for all nucleotides.

Calculate Distance Between Residues#

Immediately, we can check if a residue pair is pi-stacking in a given frame. We calculate the distance between the COG of two residues using calculate_residue_distance(). COG distance close to 3.5 Å indicates pi-stacking. For instance, the A-site mRNA codons (residues 422, 423, and 424) are likely pi-stacking:

>>> distance_vec = st.calculate_residue_distance(
...     filtered_traj,
...     res1 = 422,
...     res2 = 423,
...     frame = 3
... )
>>> distance_vec.magnitude()
3.509042

Create a System Stacking Fingerprint (SSF)#

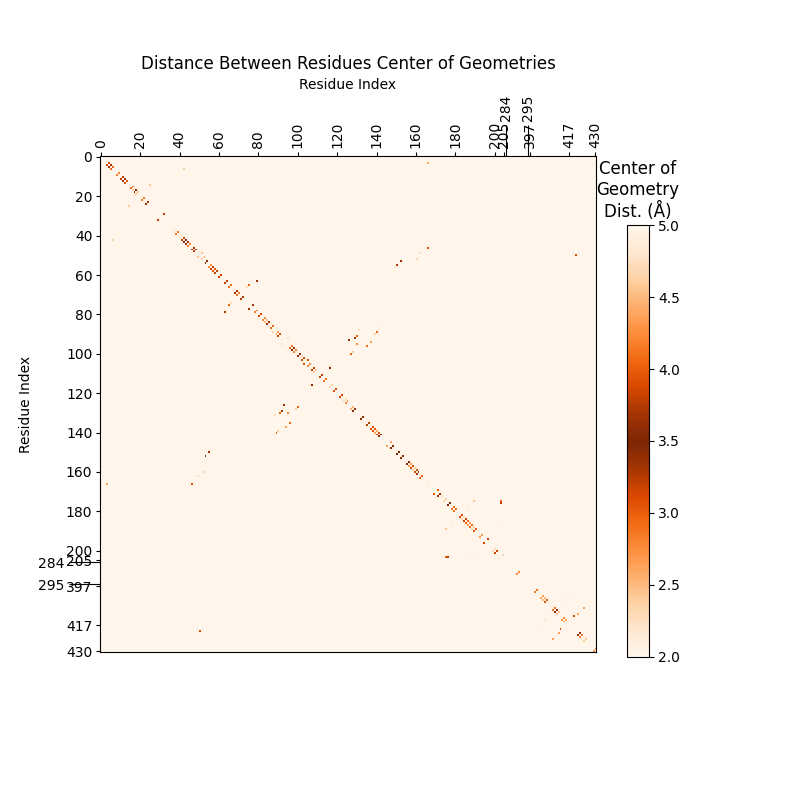
An SSF calculates the COG distance for all nucleotide pairs in a trajectory frame. The result is a square matrix where position (i, j) represents the distance from residue i to residue j. This is done with get_residue_distance_for_frame()

The filtered_traj object has 252 residues, so we create a 252 x 252 SSF:

>>> ssf = st.get_residue_distance_for_frame(filtered_traj, frame = 2, write_output = True)
Loading: [####################################################################################################] Current Residue: 252/252 (100.0%)
Frame 2 done.
>>> ssf.shape
(252, 252)

We can calculate the SSF for multiple frames of a trajectory using system_stacking_fingerprints(), which accepts smart indexing of frames (eg. 1-3,15-17 = 1,2,3,15,16,17):

>>> ssfs = st.system_stacking_fingerprints(filtered_traj, frames = '1-3')
>>> ssfs.shape
(3, 252, 252)

ssfs is now a list, where ssfs[i] is the SSF for frame i (0-indexed frame). If frames is empty, the SSF will be calculated for all frames. For multi-frame trajectories, it is recommended to use the threads option to parallelize, calculating the SSF for multiple frames at once. When parralelizing, turn off standard output with write_output:

>>> ssfs = st.system_stacking_fingerprints(
...     filtered_traj,
...     frames = '1-10',
...     threads = 10,
...     write_output = False
... )
>>> ssfs.shape
(10, 252, 252)

Get the Average SSF for a Trajectory#

Single-frame SSFs are rarely as illuminating as the average SSF for all frames of a trajectory. Users can create this using get_frame_average(), using the output from system_stacking_fingerprints() in the step above:

>>> ssfs = st.system_stacking_fingerprints(
...     filtered_traj,
...     frames = '1-10',
...     threads = 10,
...     write_output = False
... )
>>> avg_ssf = st.get_frame_average(ssfs)
>>> avg_ssf.shape
(252, 252)

avg_ssf contains averaged stacking information throughout the trajectory. The next step shows how to analyze these results.

How to Visualize an SSF#

display_ssfs() will visualize SSFs in Python output, with each SSF frame as a frame of the video:

>>> import stacker as st
>>> filtered_traj = st.filter_traj("first10_5JUP_N2_tUAG_aCUA_+1GCU_nowat.mdcrd",
...                 top_file = "5JUP_N2_tUAG_aCUA_+1GCU_nowat.prmtop",
...                 atoms = {"C2", "C4", "C6"})
WARNING: Residue Indices are expected to be 1-indexed
Reading trajectory...
Reading topology...
Filtering trajectory...
WARNING: Output filtered traj atom, residue, and chain indices are zero-indexed
>>> ssfs = st.system_stacking_fingerprints(
...     filtered_traj,
...     frames = '1-10',
...     threads = 10,
...     write_output = False
... )
>>> resSeqs = [res.resSeq for res in filtered_traj.topology.residues]
>>> st.display_ssfs(
...     ssfs,
...     res_indicies = resSeqs,
...     seconds_per_frame = 2
... )

It is recommended to run get_frame_average() and then save the output as a .png for comparison with other trajectories:

>>> import stacker as st
>>> filtered_traj = st.filter_traj("first10_5JUP_N2_tUAG_aCUA_+1GCU_nowat.mdcrd",
...                 top_file = "5JUP_N2_tUAG_aCUA_+1GCU_nowat.prmtop",
...                 atoms = {"C2", "C4", "C6"})
WARNING: Residue Indices are expected to be 1-indexed
Reading trajectory...
Reading topology...
Filtering trajectory...
WARNING: Output filtered traj atom, residue, and chain indices are zero-indexed
>>> ssfs = st.system_stacking_fingerprints(
...     filtered_traj,
...     frames = '1-10',
...     threads = 10,
...     write_output = False
... )
>>> avg_ssf = st.get_frame_average(ssfs)
>>> ssfs = [avg_ssf]
>>> resSeqs = [res.resSeq for res in filtered_traj.topology.residues]
>>> st.display_ssfs(
...     ssfs,
...     resSeqs,
...     tick_distance = 20,
...     outfile = "SSF_test.png",
...     scale_limits = (2,5),
...     xy_line = False
... )
_images/SSF_test.png

Command Line Options offers many future analyses, including combining SSF images along the x=y line for visual comparison with stacker -s ssf -B and stacker -s compare.

How to Analyze an SSF#

get_top_stacking() will give the stacking pairs with the most pi-stacking (ie. closest to 3.5Å):

>>> st.get_top_stacking(
...     filtered_traj,
...     avg_ssf
...     )
Res1    Res2    Avg_Dist
117     108     3.43
153     54      3.35
56      151     3.34
94      127     3.67
93      130     3.68

It is recommended to save the output to a .csv and use the other parameters for get_top_stacking() to prepare for future analyses using the Command Line Options:

>>> st.get_top_stacking(
...     filtered_traj,
...     avg_ssf,
...     csv = 'top_stacking.csv',
...     n_events = -1,
...     include_adjacent = True
... )

In the command line, [user]$ stacker -s compare can give the residue pairs that changed the most between trajectories, by inputting two csv outputs from get_top_stacking(). Use [user]$ stacker -s compare --help for more information.

Using K Means#

You can compare multiple System Stacking Fingerprints via K-Means. The algorithm takes multiple SSFs with no knowledge of their trajectory and groups similar SSFs. Thus, the algorithm groups trajectories via similar system-wide stacking.

Note: the SSFs must be comparable, meaning an equal amount of residues.

With StACKER’s Command Line Options, the .txt files below were created:

  • testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz : numpy array with 3200 SSFs

  • testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz : numpy array with 3200 SSFs

These files are too large to provide, but can be made with stacker -s ssf -d.

They can be read as Python objects and reshaped:

>>> import numpy as np
>>> import math
>>> GCU_3200_flattened_ssfs = np.loadtxt('../testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz')
>>> GCU_3200_flattened_ssfs.shape
(3200, 16129)
>>> GCU_3200_ssfs = GCU_3200_flattened_ssfs.reshape(GCU_3200_flattened_ssfs.shape[0], math.isqrt(GCU_3200_flattened_ssfs.shape[1]), math.isqrt(GCU_3200_flattened_ssfs.shape[1]))
>>> GCU_3200_ssfs.shape
(3200, 127, 127)
Or the files can be read and prepared for KMeans data

with read_and_preprocess_data() and run_kmeans():

>>> import stacker as st
>>> data_arrays  = st.read_and_preprocess_data(
...     ["testing/5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz",
...     "testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz"]
... )
>>> st.run_kmeans(data_arrays, n_clusters = 2)
(6400, 16129)
For n_clusters = 2 The average silhouette_score is : 0.10815289849518733
Dataset: 5JUP_N2_tGGG_aCCU_+1CGU_data
        Cluster 1: 0 matrices
        Cluster 2: 3200 matrices
Dataset: 5JUP_N2_tGGG_aCCU_+1GCU_data
        Cluster 1: 3120 matrices
        Cluster 2: 80 matrices

So the SSFs from the two datasets are distinct enough to separate into two clusters. We can visualize this with plot_cluster_trj_data():

>>> import stacker as st
>>> data_arrays  = st.read_and_preprocess_data(
...     ["testing/5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz",
...     "testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz"]
... )
>>> st.run_kmeans(data_arrays, n_clusters = 7, outdir = 'testing/')
(6400, 16129)
For n_clusters = 7 The average silhouette_score is : 0.09968523895626617
Dataset: 5JUP_N2_tGGG_aCCU_+1CGU_data
        Cluster 1: 560 matrices
        Cluster 2: 0 matrices
        Cluster 3: 240 matrices
        Cluster 4: 0 matrices
        Cluster 5: 1138 matrices
        Cluster 6: 2 matrices
        Cluster 7: 1260 matrices
Dataset: 5JUP_N2_tGGG_aCCU_+1GCU_data
        Cluster 1: 80 matrices
        Cluster 2: 1057 matrices
        Cluster 3: 0 matrices
        Cluster 4: 738 matrices
        Cluster 5: 0 matrices
        Cluster 6: 1245 matrices
        Cluster 7: 80 matrices
Results written to: testing/clustering_results_7.txt
>>> st.plot_cluster_trj_data("testing/clustering_results_7.txt", "testing/kmeans_plot.png", {'5JUP_N2_tGGG_aCCU_+1CGU_data': 'tGGG_aCCU_+1CGU', '5JUP_N2_tGGG_aCCU_+1GCU_data': 'tGGG_aCCU_+1GCU'})
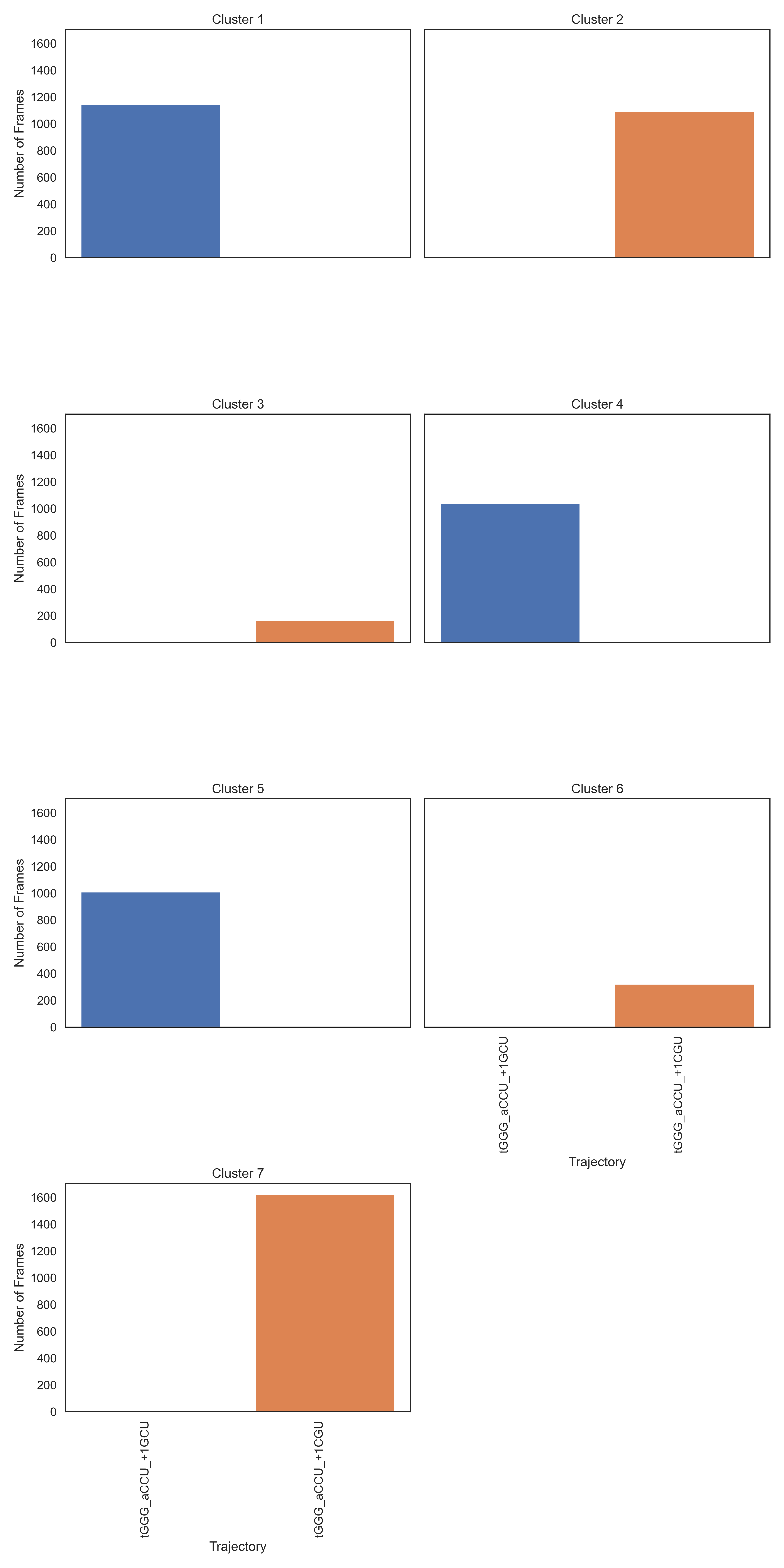
_images/kmeans_plot.png

The SSFs still split into distinct clusters (there is no cluster with a significant contribution from both trajectories), meaning the structures have different pi-stacking.

Picking the Right Number of Clusters#

StACKER is equipped to run Silhouette Analysis in order to select the correct number of clusters. plot_silhouette() can create Silhouette Plots:

>>> import stacker as st
>>> data_arrays  = st.read_and_preprocess_data(
...     ["testing/5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz",
...     "testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz"]
... )
Reading data: 5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz
Reading data: 5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz
>>> blinded_data = st.create_kmeans_input(data_arrays)
(6400, 16129)
>>> for n_cluster in range(2,8):
...     st.run_kmeans(data_arrays, n_clusters = n_cluster, outdir = 'testing/')
...     st.plot_silhouette(n_cluster, blinded_data, outdir = 'testing/')
(6400, 16129)
For n_clusters = 2 The average silhouette_score is : 0.10815289849518733
Dataset: 5JUP_N2_tGGG_aCCU_+1CGU_data
        Cluster 1: 0 matrices
        Cluster 2: 3200 matrices
Dataset: 5JUP_N2_tGGG_aCCU_+1GCU_data
        Cluster 1: 3120 matrices
        Cluster 2: 80 matrices
Results written to: ../testing/clustering_results_2.txt
File saved to: ../testing/silhouette2.png
(6400, 16129)
For n_clusters = 3 The average silhouette_score is : 0.11018525011212786
Dataset: 5JUP_N2_tGGG_aCCU_+1CGU_data
        Cluster 1: 720 matrices
        Cluster 2: 0 matrices
        Cluster 3: 2480 matrices
Dataset: 5JUP_N2_tGGG_aCCU_+1GCU_data
        Cluster 1: 0 matrices
        Cluster 2: 3194 matrices
        Cluster 3: 6 matrices
Results written to: ../testing/clustering_results_3.txt
File saved to: ../testing/silhouette3.png
...

Silhouette Plots show the distance of all points in a cluster from the cluster’s centroid. We want plots with clusters of similar size along the y-axis and with most points around the same distance from 0 on the x-axis. A Cluster choice of 6 is appropriate:

testing/silhouette6.png

_images/silhouette6.png

While a cluster choice of 7 is not:

testing/silhouette7.png

_images/silhouette7.png

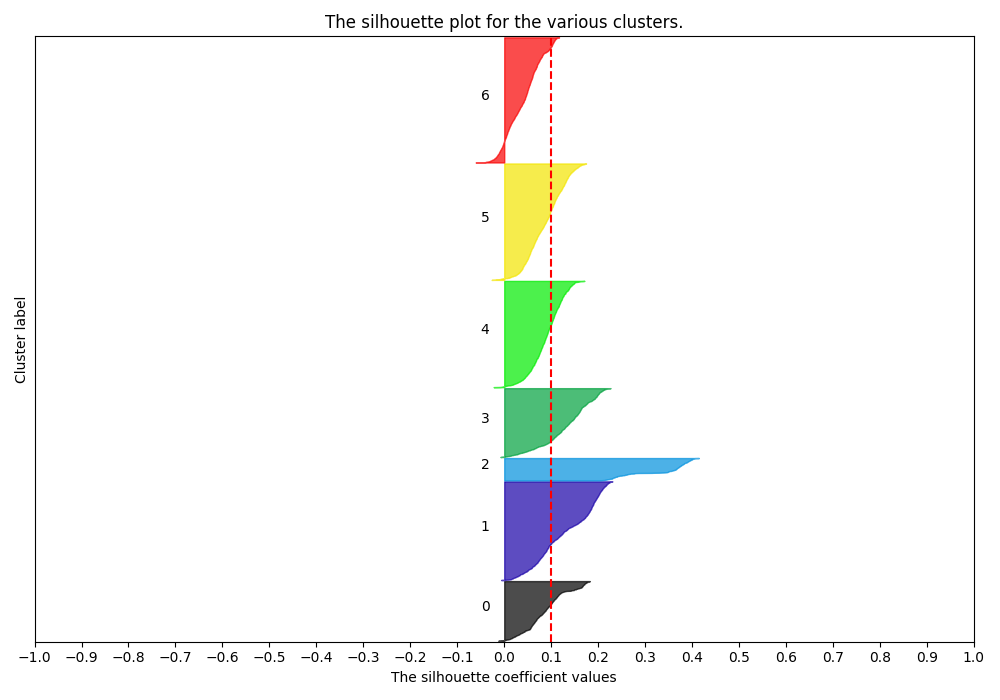
Principal Component Analysis#

KMeans on SSF gathers Euclidean Distance on multi-dimensional vectors that are impossible to plot. We can, however, do a heuristic plotting of these SSFs using Principal Component Analysis (PCA).

First, we can plot the un-blinded SSFs and color them by their trajectory of origin. We have 3200 frames worth of SSFs for each trajectory, and we plot them using plot_pca():

>>> import stacker as st
>>> dataset_names = ["testing/5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz",
...     "testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz"]
>>> data_arrays  = st.read_and_preprocess_data(
...     dataset_names
... )
Reading data: 5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz
Reading data: 5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz
>>> blinded_data = st.create_kmeans_input(data_arrays)
(6400, 16129)
>>> st.plot_pca(blinded_data, dataset_names, 'dataset')

This creates a PCA plot where each point is a frame of a trajectory, plotted using the information solely from the SSF. The points are colored by the trajectory dataset of origin. This outputs to a .png:

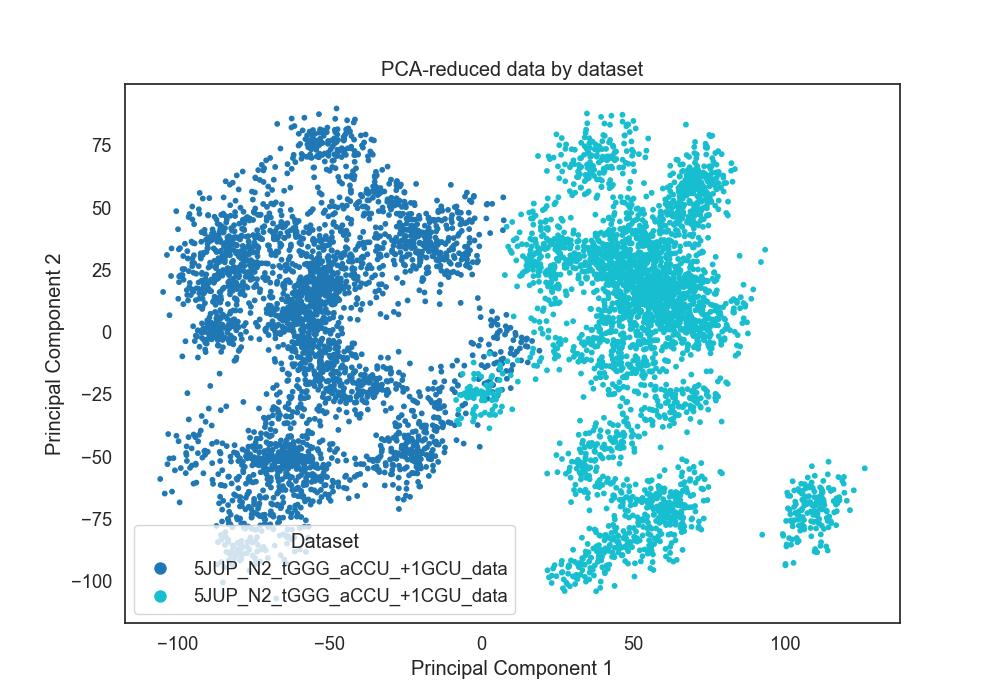
_images/pca_plot.by_dataset.png

Here the SSFs from the two datasets separate cleanly, indicating significantly different system-wide stacking. The PCA Plots can also be colored by kmeans result. Here, the frames are colored by their KMeans result with 6 clusters:

>>> import stacker as st
>>> data_arrays  = st.read_and_preprocess_data(
...     ["testing/5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz",
...     "testing/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz"]
...     )
Reading data: 5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz
Reading data: 5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz
>>> blinded_data = st.create_kmeans_input(data_arrays)
(6400, 16129)
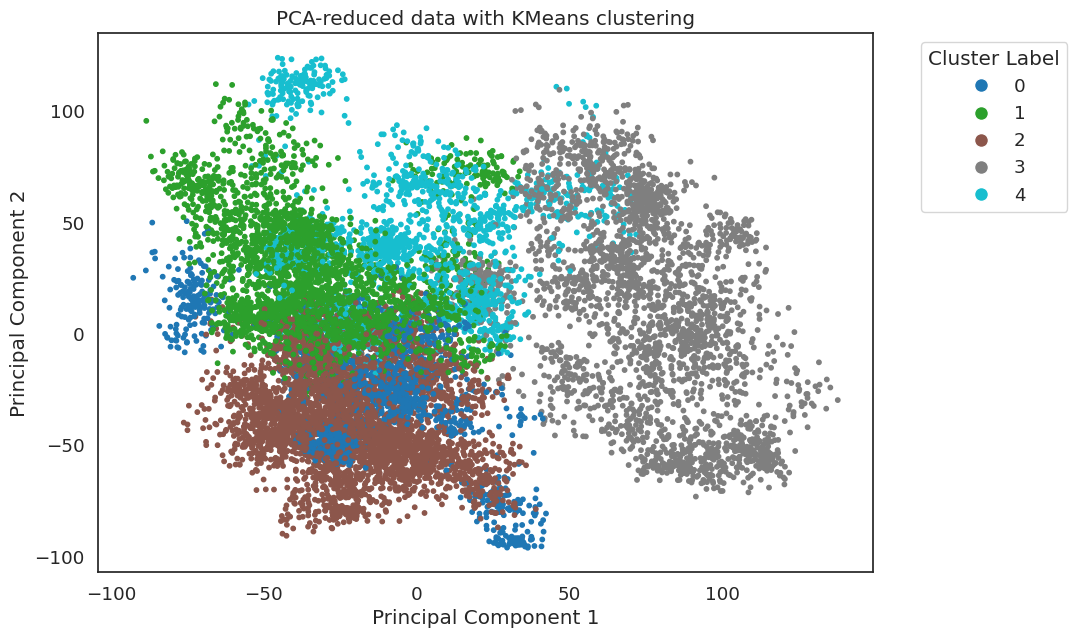
>>> kmeans_results = st.run_kmeans(data_arrays, n_clusters=6)
(6400, 16129)
For n_clusters = 6 The average silhouette_score is : 0.09343055568735036
Dataset: 5JUP_N2_tGGG_aCCU_+1CGU_data
        Cluster 1: 0 matrices
        Cluster 2: 0 matrices
        Cluster 3: 1459 matrices
        Cluster 4: 4 matrices
        Cluster 5: 1017 matrices
        Cluster 6: 720 matrices
Dataset: 5JUP_N2_tGGG_aCCU_+1GCU_data
        Cluster 1: 1179 matrices
        Cluster 2: 824 matrices
        Cluster 3: 0 matrices
        Cluster 4: 1197 matrices
        Cluster 5: 0 matrices
        Cluster 6: 0 matrices
>>> st.plot_pca(blinded_data, dataset_names, coloring = 'kmeans', cluster_labels=kmeans_results)
_images/pca_plot6by_cluster.png

Each trajectory has three clusters, with no cluster capturing significant frames from both trajectories.

Finally, they can be colored by dataset but use facet to show each dataset’s points on a separate PCA Grid. This helps with viewing multiple datasets:

>>> import stacker as st
>>> dataset_names = ["/home66/esakkas/STACKER/DATA/5JUP_N2_tGGG_aCCU_+1CGU_data.txt.gz",
...     "/home66/esakkas/STACKER/DATA/5JUP_N2_tGGG_aCCU_+1GCU_data.txt.gz",
...     "/home66/esakkas/STACKER/DATA/5JUP_N2_tGGG_aCCC_+1CGU_data.txt.gz",
...     "/home66/esakkas/STACKER/DATA/5JUP_N2_tGGG_aCCC_+1GCU_data.txt.gz"
...     ]
>>> data_arrays = st.read_and_preprocess_data(dataset_names)
>>> blinded_data = st.create_kmeans_input(data_arrays)
(12800, 16129)
>>> st.plot_pca(blinded_data, dataset_names, 'facet')
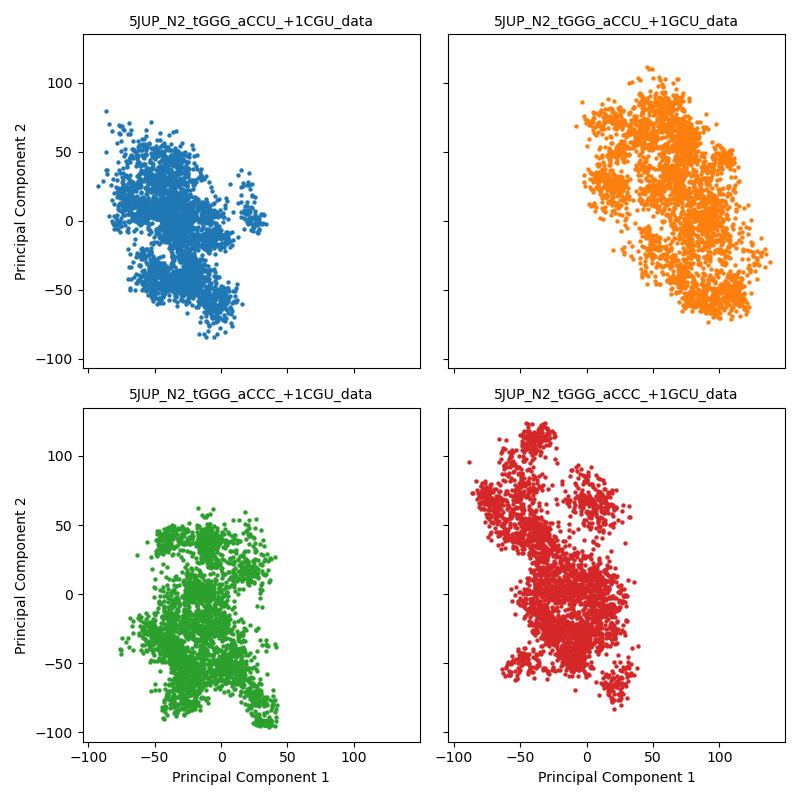
_images/pca_plot.by_facet.png

Here we see that the tGGG_aCCU_+1GCU trajectory occupies its own space. We can combine this result with the KMeans and PCA plots below to strongly support the conclusion that tGGG_aCCU_+1GCU has a different system-wide stacking, and therefore a different structure, than the other three trajectories. The K-Means results with the best silhouette plot is shown here:

_images/silhouette5.png _images/kmeans5.png _images/pca_plot5by_cluster.png